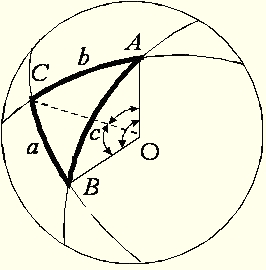
Трикутник, утворений дугами великих кіл, називається сферичним. Кути позначаються великими буквами (A,B,C...), вимірюються кутами між дотичними до дуг великих радіусів, що утворюють кут. Сторони, що лежать напроти деякого кута (напр. А), позначаються цією ж буквою, але малою (а). Сторона вимірюється центральним кутом, що спирається на дугу великого кола. Сума кутів сферичного трикутника завжди більше двох прямих і залежить від площі трикутника. Переважно розглядають сферичний трикутник з сторонами не більше 90^о. Між кутами і сторонами сферичного трикутника можна встановити ряд співвідношень: формули синусів і косинусів.

Формула косинусів

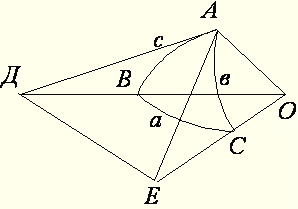Розглянемо сферичний трикутник АВС, сторони в і с якого менші 90^о. Проведемо в т.А дотичні до сторін до перетину їх з продовженням радіусів сфери ОВ, ОС в т.D i т.E. Приймемо радіус сфери за 1 (одиницю). З прямокутних трикутників DAO i EAO отримуємо:

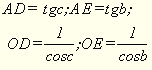(1)

З трикутників ADE i ODE знаходимо квадрат сторони DE:

(2)-(3)

Прирівнюємо (2) і (3) і переставляємо члени:

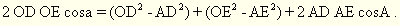(4)

Підставимо (1) в (4):

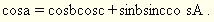(5)

З допомогою кругової підстановки в 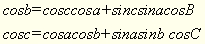(5):

(5’)

Теорема косинусів: косинус сторони сферичного трикутника дорівнює сумі добутків косинусів двох інших сторін і добутку синусів цих же сторін, помноженого на косинус кута протилежного шуканій стороні.

Формула синусів

Отримаємо її шляхом перетворення формули косинусів (5).

З (5)

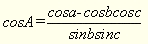(6)

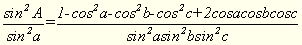
і це, у зв’язку з симетрією а,b,с дорівнює:

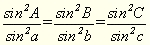(7)

З (7) випливає

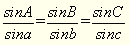(8)

Теорема синусів: синуси кутів сферичного трикутника пропорційні синусам протилежних сторін.

Формула п’яти елементів (без доведення): добуток синуса однієї сторони на косинус прилеглого кута дорівнює добутку синуса другої сторони, яка прилягає до цього кута на косинус третьої сторони, мінус добуток обернених функцій цих сторін на косинус кута між ними.

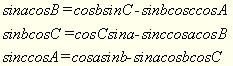(9)